明捷:数学漫谈,挑战极限的人(1)

《明捷数学随谈:挑战极限的人(1)》
By 明捷
明捷是我的高中同学,跳级来到我们高中的尖子班,学霸。令人瞩目的是数学成绩格外突出,这一定有遗传的因素,明捷的父亲是大学数学教授,母亲是高中数学教师。在1980年的高考中,明捷的成绩名列前茅。他就读于中国科技大学,后来又在中美两国获得硕士和博士学位。目前他在最著名的汽车公司工作,业余时间,还会对数学念念不忘。在高中微信群里,他写了一些在数学领域挑战极限的人和事,十分有趣,大家建议他整理成文,发表出来,让更多的人看到。不负众望,一篇《明捷数学随谈:挑战极限的人》一文,应运而生了。他没有注册任何网站,我就受他之托,将此文分享给大家。下面就是全文之一
【一.纯数学】
上世纪一位数学权威,英国剑桥大学教授哈代曾说过:“大体上讲,有用的数学都是肤浅的数学”。这里说的“有用的数学”大概是指应用数学。哈代的言下之意是,只有纯数学才是数学家真正的竞技场。其暗含的意思也是相当残酷的,即献身纯数学的数学家有可能一生离群索居,穷困潦倒,因为他们做的东西短期内没有应用价值,大多数情况下都不会引起社会关注,不会带来经济收益。他们中间的幸运者,年青时在大学和专业研究机构谋到稳定的职位,生活虽不富有,却很舒适,能够一生专注于纯数学研究。但并非所有人都有这样的幸运。
【二.数论与歌德巴赫猜想】
数学中古老的难题大都与数论相关,其表述很浅显,具有初中数学知识就可以明白,但严格证明却极其困难。如我们这一代人耳熟能详的哥德巴赫猜想,表述为:任何一个大偶数都可以写成两个素数之和。如8=3+5,48=17+31,等等,如果有时间和耐心,可以一直验算下去,直至几十亿,几百亿,但这样验证的数字再大,都不能证明该猜想。著名数学家陈景润呕心沥血,一生的时间和精力都放在哥德巴赫猜想上,仍没能证明它。但他取得了迄今世界上最领先的成果,证明了:任何一个大偶数都可以表示为一个素数和不超过两个素数的乘积之和。如6=2+2×2,8=2+2×3,10=3+7等等。

1977年,作家徐迟发表的长篇报告文学《哥德巴赫猜想》,在民间引发了巨大的反响。这篇长文不仅让人们知道了陈景润这个悲情数学家,也让人知道还有报告文学这样一种写作方式,更让当时的有志青年们了解到人生除了走革命道路外,还可以选择钻研数学,成名成家。停顿十年后于当年恢复的高考,数学系得到了最好的生源。只是不知道当年报考数学系的高材生们,有多少人最后选择了数学研究作为他们的终生职业。
【三.怀尔斯与费马大定理】
中国古人在研究直角三角形时发现了"勾三,股四,弦五",即32+42=52。其实还有很多类似的边长为整数的直角三角形,如(5,12,13),52+122=132。西方人将勾股定理称为毕达哥拉斯定理。300多年前,法国数学家费马想在毕达哥拉斯定理的基础上玩点数字游戏,他想如果该等式的幂次不是二次,而是更高次,会不会也存在类似二次时的三整数组合来满足方程呢?例如在方程a3+b3=c3中,是否存在a,b,c同为整数的解呢?他尝试后,发现找不到整数解。在更高次下,同样没找到整数解。经过反复思考后,他提出:在方程an+bn=cn中,当n>2时,不存在a,b, c同为整数的解。他在一本书的边框上写下了一段话,声称他找到了一个很妙的方法来证明这个定理,但证明过程写不下。后来人们习惯上将这个定理称为费马大定理。接下来的300多年,一代又一代的数学家费尽心思,都无法证明这个定理。他们普遍认为费马当年所说的那个"很妙的证明"一定是错的。
转眼到了19世纪末,一位年轻的德国企业家为情所困,决定自杀。自杀前的那天晚上,他莫名其妙地想去证明费马大定理,整整一个通宵,突然发现已经错过了原定自杀的时间,于是放弃了自杀方案。1908年,他临终时嘱咐从遗产中拿出10万马克,悬赏在接下来100年中能够证明费马大定理的人。
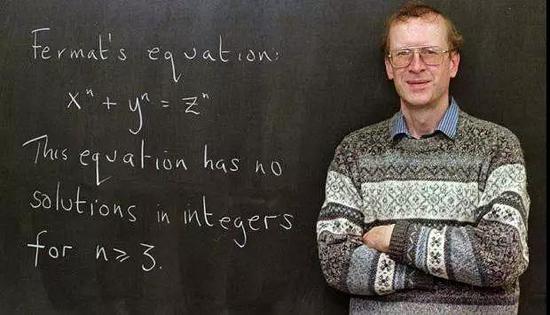
20世纪中叶,英国一个学童偶然知道了费马大定理,鬼使神差地立志要证明它,他就是安德鲁. 怀尔斯(Sir Andrew John Wiles,出生于1953年4月11日)。成年后,他理所当然地选择数学为终生职业。多年以后,他任教于普林斯顿大学,住在家里的阁楼上研究费马大定理,只有他的妻子知道他在干嘛。1993年,他声称证明了该定理,但证明过程公布后,被人指出存在缺陷。接下来一年时间,他都在致力于完善该证明。突然有一天,脑海中灵光闪现,一个简洁漂亮的想法出现了。多年后他面对采访者回忆当时的情形,仍抑制不住激动。他说当时整整一天,他都沉浸在难以描述的美感之中。他的证明终于被举世公认。怀尔斯对数学的最大贡献是证明了歷时350多年的、著名的费马猜想。
顺便说一句,和所有的研究成果一样,怀尔斯的成就是因为站在前人的肩膀上。对怀尔斯影响最大的是上世纪50年代日本青年数学家谷山的研究工作。不幸的是,谷山年纪轻轻就突然自杀,随后,他的未婚妻也自杀殉情。纯数学领域部分从业人员的生存状态,也许由此可见一斑。
【四.拉马努金的公式】
1887年,印度南部一个叫拉马努金的婆罗门家族出生了一个男婴。以后发生的一切表明,这个孩子是专门为数学而生的。婆罗门在印度种姓制度中属最高一级,但并不意味着他们都富有。事实上,这个家庭就属于贫困一类的。当小拉马努金快10岁时,已经完全沉浸在对数学的兴趣中。这时家里住进两个大学生租客,小男孩一有空就去找这两个大学生讨论数学问题。很快,大学生的数学知识就不足以应付他了。他们甩给小拉一本《高等三角学》,说这本书我们也有不明白的,你自己去读吧。小拉很快就研究完了这本书,他发现正弦和余弦函数不仅是直角三角形中直角边和斜边之比这么简单,他们和自然对数的底以及单位虚数之间存在一个奇妙的关系,小拉当时不知道的是,这其实就是著名的欧拉公式,150年前就被大数学家欧拉发现了。后来小拉又得到一本叫做古今公式大全的书,列举了几千个数学公式,他整天忙着证明推广这些公式。

转眼要考大学了,小拉连着两年都没考上,第三年总算考进了一所大学,但因为严重偏科,挂了多门课,被学校劝退了。那时他的唯一财富就是一本厚厚的笔记,里面写满了他自己发现的公式。他抱着这个笔记本四处找工作,却没人把它当回事。后来,他托人将笔记拿给当时印度数学学会的会长,会长也看不懂。但凭直觉,他意识到这个年轻人非同寻常。会长的正式职业是税务局的官员,他将拉马努金安排进税务局,这是个闲职,即解决了小拉的财务困境,又能给他足够的时间研究数学。

随着拉马努金在印度数学界名气的增大,有人建议他到英国深造。他给当时的几个英国数学权威写信自荐,其中包括剑桥大学教授哈代。哈代看到他的那些公式,立即决定邀请他去剑桥。与拉马努金见面后,哈代进一步了解了他作的研究,惊为天人。他形容和拉马努金的相识,是“生命中的一次浪漫”。由于拉马努金没有经过系统的专业训练,即使在数学领域,他的知识也是残缺的,但这并不影响他成为一个伟大的数学家。他凭直觉写下的那些公式,令人匪夷所思。当时很多人惊奇他是怎么想到这些公式的,他说是睡梦中神给他的启示。我第一次看到拉马努金的那些公式时,感觉就是两个字:震撼。一种谦卑感从心底由然而生。感觉到还存在另一个我毫无所知的数学世界,而拉马努金就是从那个世界穿越过来的人。有人用“宏伟的公式”形容拉马努金的作品,毫不过分。遗憾的是,早年的贫困生活和过度专注的研究,毁坏了拉马努金的身体,使他在32岁时就离开了人世。
值得一提的是,数学公式通常都是经过严格推导得出。但拉马努金的那些公式,都是他直接写出来的,没有推导过程。有人后来试图证明他的一些公式,发现都是对的。但他写下的公式太多了,还有很多留待后人证明。后来人们创办了一个数学期刊,称为《拉马努金杂志》,用来发表与他那些公式相关的研究工作。
爱因斯坦的一句话在拉马努金的身上得到了验证:想象力比知识更重要。或许人们无法拥有像拉马努金一样的直觉,但是,只要我们能够放飞自己的想象里,看到的世界一定更加美好!
(照片来自网络)
